Miscellaneous Tools

Listed here are some of the various tools and other miscellany I developed for music theory and analysis while at the Eastman School of Music.

Dissertation Defense Presentation

For the presentation that I gave before the defense of my dissertation, I avoided PowerPoint altogether, using instead impress.js as the main engine of my slideshow. Included within the slideshow are some examples that exploit my plot-pc-set.js script to demonstrate how the z-relation works. Unlike usual web-based slideshows, it is a dynamic hands-on slideshow.

Set Class Ear-Trainer

The first version of my set class ear-trainer is a Java applet and desktop application. Thusfar, it has been quite successful and well received. Recently, however, I decided to rewrite the program as a pure Javascript web page. Unfortunately, the project was a little more frustrating than first expected, since MIDI is not well supported by modern browsers. The new webapp that I came up with uses jasmid.js to create the sound on-the-fly. It is fantastic that this is even possible; the drawback, however, is that it works only with FireFox or Chrome.

Mobile Music Calculator

This webapp is a mobile app that uses JQTouch along with Zepto. It is a suite of music calculators, which now includes a set class calculator and a twelve-tone matrix builder. Personally, when analyzing music, I use this webapp all the time.

Set Class Calculator

This calculator uses AJAX to query the server about information about set classes. It is a bit old, and could certainly be improved, but it serves as a good example of of some of my earlier work, which has the server respond with information according to set-class lists stored server-side. Overall, this calculator is very powerful, in that it responds relatively quickly with hard-to-calculate information.

plot-pc-set.js

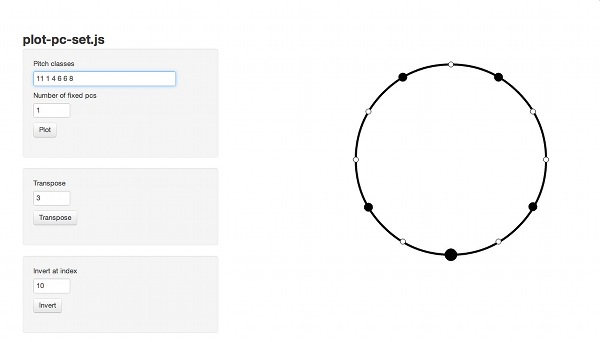
This script is a javascript module available at github. It allows the user to easily include set-class graphs on their web page, and to animate certain transformations, such as transposition and inversion. This script was used in the slideshow of the presentation given for my dissertation defense.

Overview

I began my studies as a student of violin at Texas Tech University. During that time, I went to Lugano, Switzerland to study with the maestro Carlo Chiarappa.

After completing my undergraduate degree at Texas Tech, I went to SUNY Buffalo and the Eastman School of Music to pursue a doctorate in music theory. My graduate research focused primarily on music of the twentieth and twenty-first centuries, and specifically on post-war composers of the European tradition, such as Elliott Carter, Luciano Berio, Witold Lutoslawski and Henri Dutilleux. I have also done research on the history of music theory (particularly Renaissance and early-Baroque theory), Schenkerian theory, and on phenomenological approaches to analysis.

During my graduate studies I also discovered programming and independently gained experience with C, Python, PHP, and Javascript, as well as with Linux servers. While at Eastman, I managed the website for the music theory department, and then became a web administrator for the Society for Music Theory. Currently, I am a Staff Software Engineer at Bestow.

The Z-Relation in Theory and Practice

My dissertation focuses on a special correspondence between music theory and crystallography, namely the z-relation. It is now available online at ProQuest.

Abstract

Though the z-relation—the relationship whereby two sets not related by transposition and/or inversion have the same interval-class content—has been one of the core concepts of pitch-class set theory since its inception, the principles underlying the relationship have to a large extent remained obscure. However, new information is emerging. First, recent work on the Fourier transform for pitch-class- set analysis (in particular, by Ian Quinn, which builds on work by David Lewin) provides new information concerning the subset structure of z-related sets. Second, as recognized by Clifton Callender and Rachel Hall, the z-relation is an instance of what crystallographers call homometry, which has been written about extensively. The aim of this study is to utilize these new means to present a comprehensive description of the z-relation that addresses the criteria upon which the z-relation relies as well as the ways in which z-related sets interrelate.

Building upon algebraic formulas suggested by crystallographers, I develop an approach that describes z-related pairs in terms of formulas that correspond to subset properties illustrated by the Fourier transform. In addition to devising my own formulas, I show that the formulas can be extended with a method called ‘pumping’ (O’Rourke, et alii), which adds pitch-classes to preformed formulas. Together, the formulas and pumping lead to a general theory of the z-relation that not only describes the relationships between the sets of a z-related pair, but also those between z-related pairs of different cardinalities.

Since it exposes transformational relationships, the algebraic approach lends itself well to the analysis of music that involves z-related sets, whether twelve-tone music based on rows with discrete hexachords that are z-related, or other non-serial music that prominently features z-related sets as motivic harmonies. In my own work I use the theory to analyze twentieth-century works by composers including Schoenberg, Berg, Carter and Berio. Overall, the theory exposes that transformational networks involving z-related sets are not only possible, but are altogether relevant to the analysis of music that involves such harmonies.

Professional Services for Hire

Though my time is mostly wrapped up by my day job, I my am generally available as an independent contractor for application development or systems administration. Feel free to contact me and I can provide an estimate.

Purchase Hours

My services come at a rate of $100/hour.

Use Bitcoin

You can purchase service hours with bitcoin on coinbase.

Use Credit Card

You can purchase service hours with your credit card using Stripe.

Note: all personal billing details are stored by Stripe. Only the Stripe tokens are stored on this server.