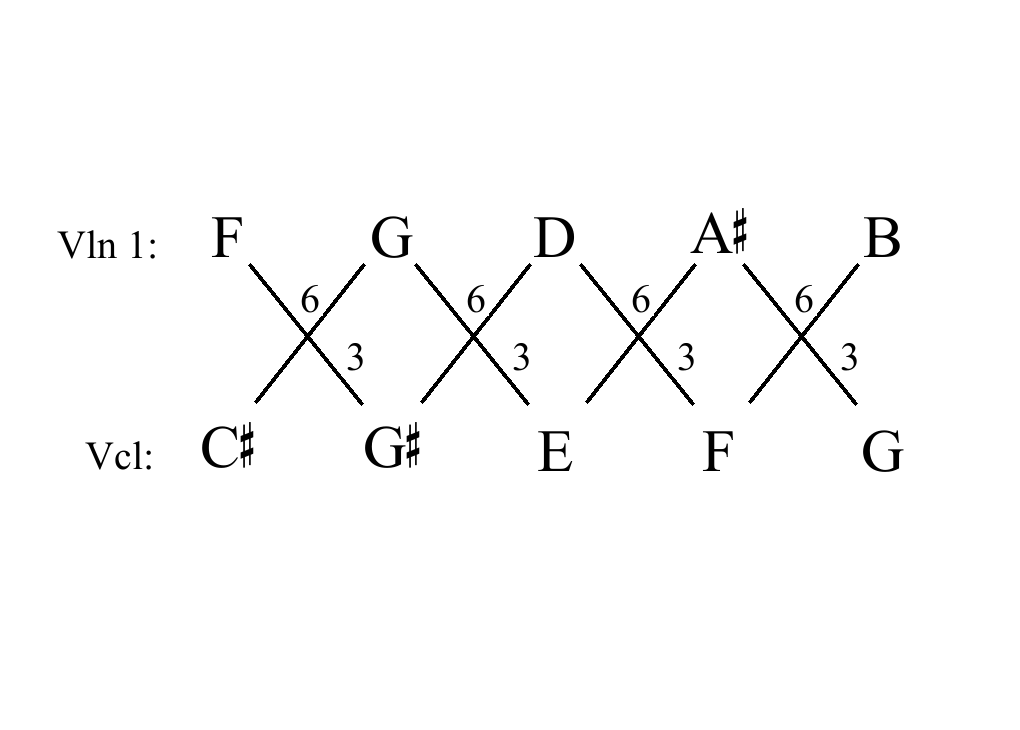The Z-Relation in Theory and Practice
Jeremiah Goyette
View slideshow at:
http://jeremiahgoyette.com/defense-presentation/
A pair of pc sets...which have identical interval vectors but which are not transpositionally or inversionally equivalent will be called a Z-related pair.
Allen Forte, The Structure of Atonal Music (1973), p. 21
23 pairs of z-related sets in mod12
Z-relation first discovered in music theory by:
| David Lewin | 1960. The Intervallic Content of a Collection of Notes, Intervallic Relations between a Collection of Notes and its Complement: an Application to Schoenberg’s Hexachordal Pieces. Journal of Music Theory 4/1: 98-101. |
| Howard Hanson | 1960. The Harmonic Materials of Twentieth-Century Music. New York: Appleton-Century-Crofts. |
Some prominent critics/commentators:
| John Clough | 1965. Pitch-Set Equivalence and Inclusion (A comment on Forte’s Theory of Set-Complexes). Journal of Music Theory 9/1: 163-180. |
| George Perle | 1982. Letter from George Perle. Journal of the American Musicological Society 35/2: 373-377. |
| 1990. Pitch-Class Set Analysis: An Evaluation. The Journal of Musicology 8/2: 151-172. |
Sets in the Z-relation will sound similar because they have the same interval-class content, but they won't be as closely related to each other as sets that are members of the same set class.
Joseph Straus, Introduction to Post-Tonal Theory
(2nd ed., 2000), p. 80


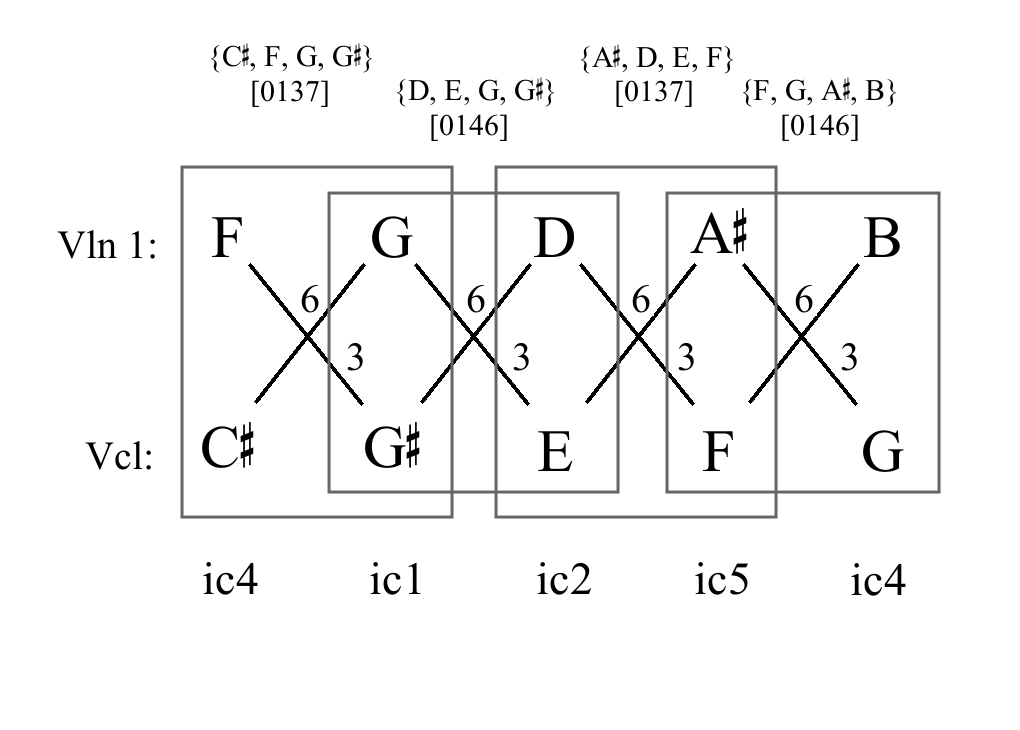
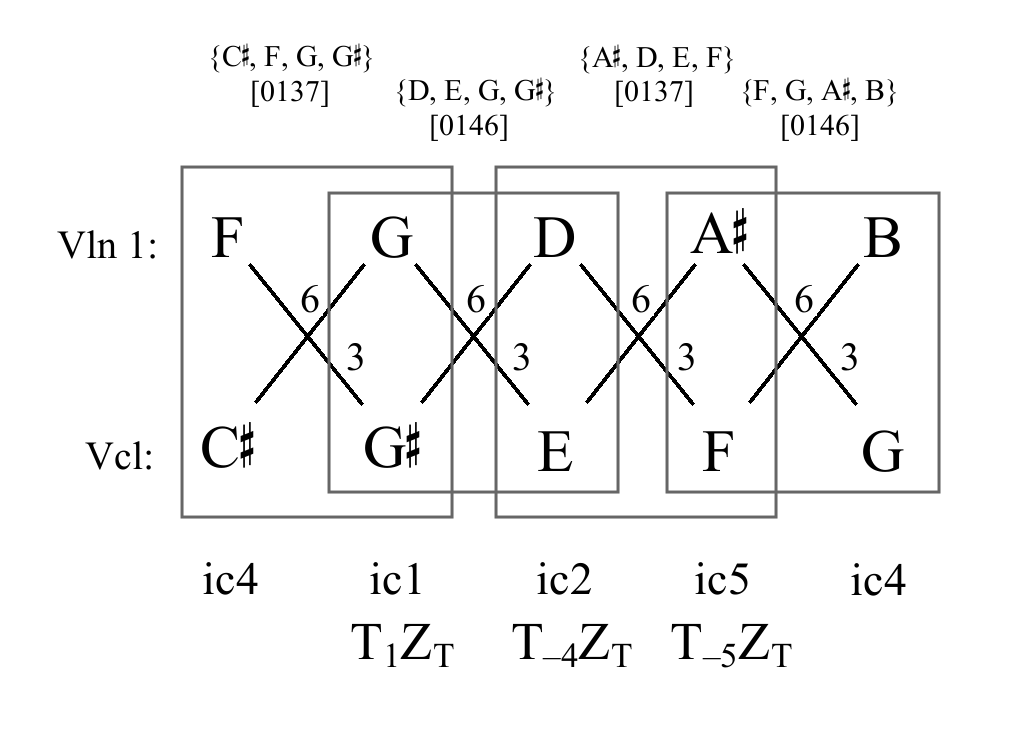
Alban Berg, op. 2 no. 4, mm. 18-22.

All-interval tetrachords sharing trichords
[016] shared
 [026] shared
[026] shared



A few questions with which to grapple
- What criteria must be met in order so that two sets of different set classes share the same interval-class content?
- Do all groups of z-related sets satisfy the same criteria, or are there different types of z-relation?
- Is it possible to enumerate the z-related sets; in other words, is it possible to calculate the number of z-related sets without having to count them either by hand or with a computer?
- Given a z-related pitch-class set, how can one derive the z-related partner?
- How can one tell if a random pitch-class set is potentially a z-related set?
Robert Morris
- Several works describing aspects of z-relation, including Composition with Pitch Classes (1987) and Class Notes for Advanced Atonal Music Theory (2001).
- By way of his ZC-relation, observed certain key properties of z-related hexachords, such as that they derive from particular subset unions.
- Observed some characteristics of the all-interval tetrachords, such as that they both arise from a non-overlapping union of [06] and [03] dyads, and that together they form an octatonic collection.
Stephen Soderberg
- "Z-Related Sets as Dual Inversion" JMT (1995).
- First substantial theory of z-relation in music theory.
- Aim is to generate z-related sets in various moduli, not just mod12.
- Methodology involves extracting z-related pairs from the 'Q-grid', a pitch-class matrix comprised of overlapping cyclic collections.
- Dual inversion – depending on which pitch classes have been chosen in the Q-grid, the z-related partner is found by inverting each of the pitch classes in one of two ways.
New information
1. Fourier transform:
- Introduced by David Lewin (1959 and 2001), and expanded by Ian Quinn (2007).
- Sets that are z-related have Fourier coefficients with the same magnitudes; that is, they are equally imbalanced on all of the Fourier balances.
- Consequently, sets that are z-related contain identical cyclic-collection subsets (e.g., [06] or [048] in mod12).
Fourier balances (Quinn 2007)
balance 1 |
balance 2 |
balance 3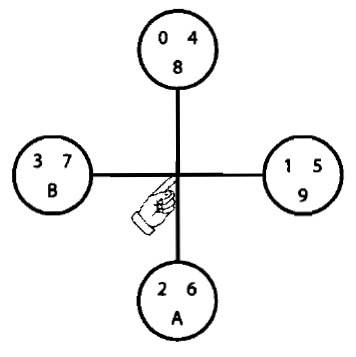 |
balance 4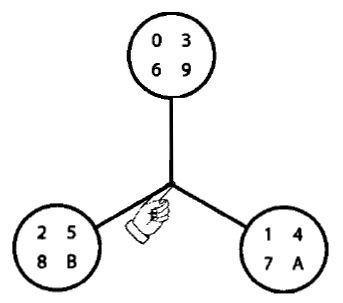 |
balance 5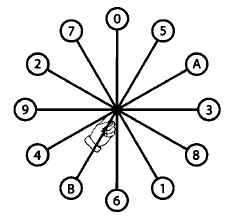 |
balance 6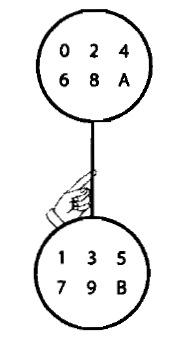 |
New information
2. Parallels to crystallography:
- Z-related sets are analogous to what crystallographers call homometric sets.
- Homometricity was first recognized in 1930 by Linus Pauling and M. D. Shappell as an obstacle in the analysis of atomic structures.
- Crystallographers have posited several mathematical explanations for homometricity, which range in scope and complexity.
Homometric pair
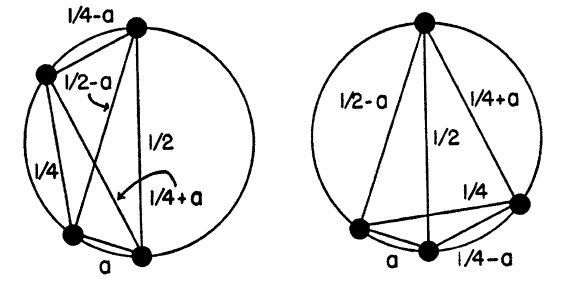
Patterson, Arthur Lindo. Ambiguities in the X-ray Analysis of Crystal Structure. Phys. Rev. 65 (1944): 195-201.
Some insights to be observed
- Homometric sets exist in a variety of periodic and linear spaces.
- There are indeed different types of homometric sets, such as Bagchi and Hosemann's (1953) distinction between homomorphs and pseudohomometric sets.
- Certain homometric pairs can be expressed as algebraic expressions. All homometric groups can be expressed as polynomial equations (Rosenblatt and Seymour 1982).
- Work on homometric sets shows that the z-related sets arise from concrete subset relationships, and thus offers a transformational perspective for the z-relation.
My contributions
- Survey of Fourier transform, and its implications for the z-relation
- Generation of algebraic z-relation formulas
- General formula (and criteria) for z-related pairs with sets that have one cyclic-collection subset.
- Pumping (from O'Rourke, et al. 2008), which adds pitch classes to the general formula to generate larger cardinality z-related pairs with more than one cyclic-collection subset.
- The 'reciprocal set union', which describes certain aggregate-forming z-related pairs (sets with cardinality of half the modulus).
- Z-transformations
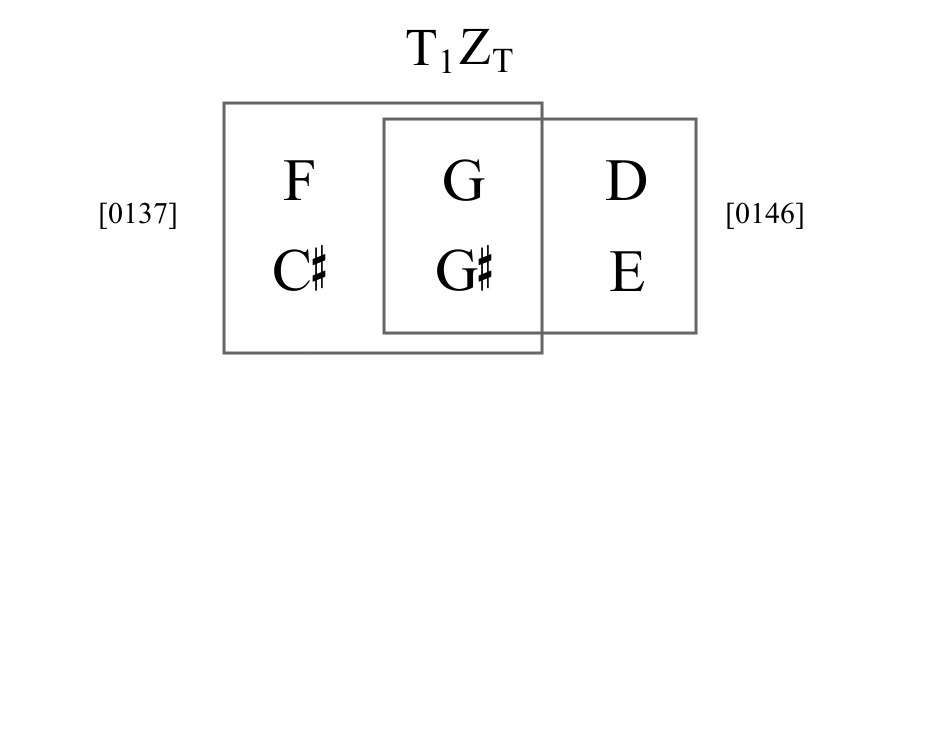
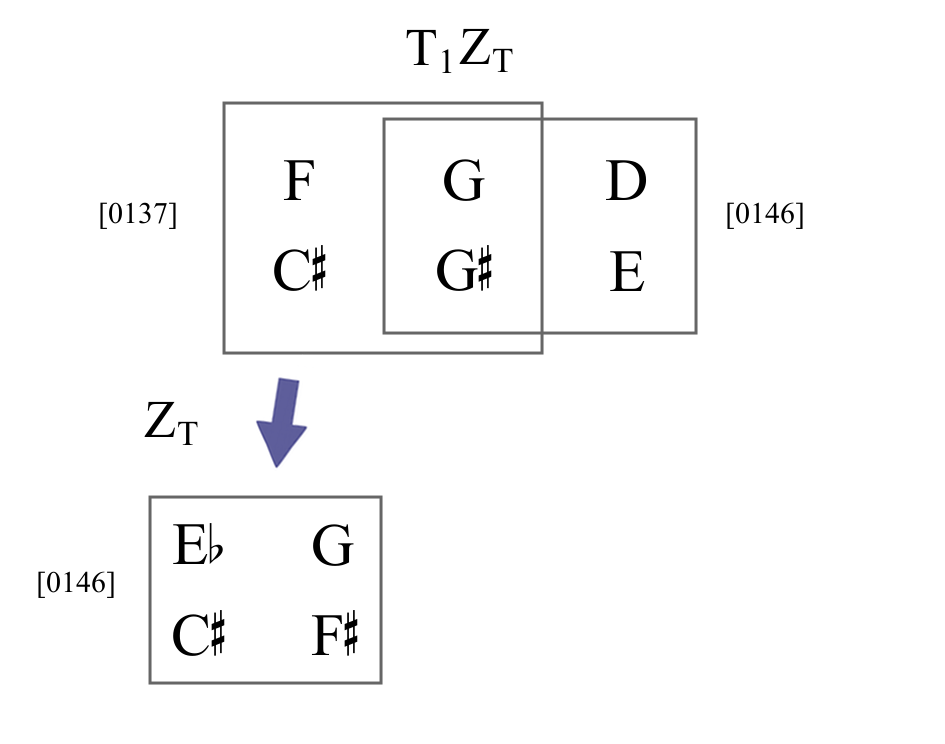
Z-transformations
- Derive from the general formula.
- Contextual transformations that change a set on one side of the formula to the set on the other.
- Three types:
- Z-transposition (ZT)
- Z-inversion (ZI)
- Cyclic-sub z-transformation (ZCS)
General z-relation formula
| set 1 | set 2 | |
Φ ⊎ x + Ψ |
Z |
Φ ⊎ −x + Ψ |
(such as [06] or [048] in mod12)
Ψ (Psi) – non-cyclic collection (remainder set)
x ∈ ℝ and x ≢ 0 (mod φ/2)
⊎ – multiset sum
{0, 6} ⊎ x + {0, 3} Z {0, 6} ⊎ −x + {0, 3} if x ≢ 0 (mod3)
[ 0 0 3 6 ]
[ 0 0 3 6 ]
{0, 6} ⊎ x + {0, 1, 5} Z {0, 6} ⊎ −x + {0, 1, 5} if x ≢ 0 (mod3)
[0 0 1 5 6 ]
[0 0 1 5 6 ]
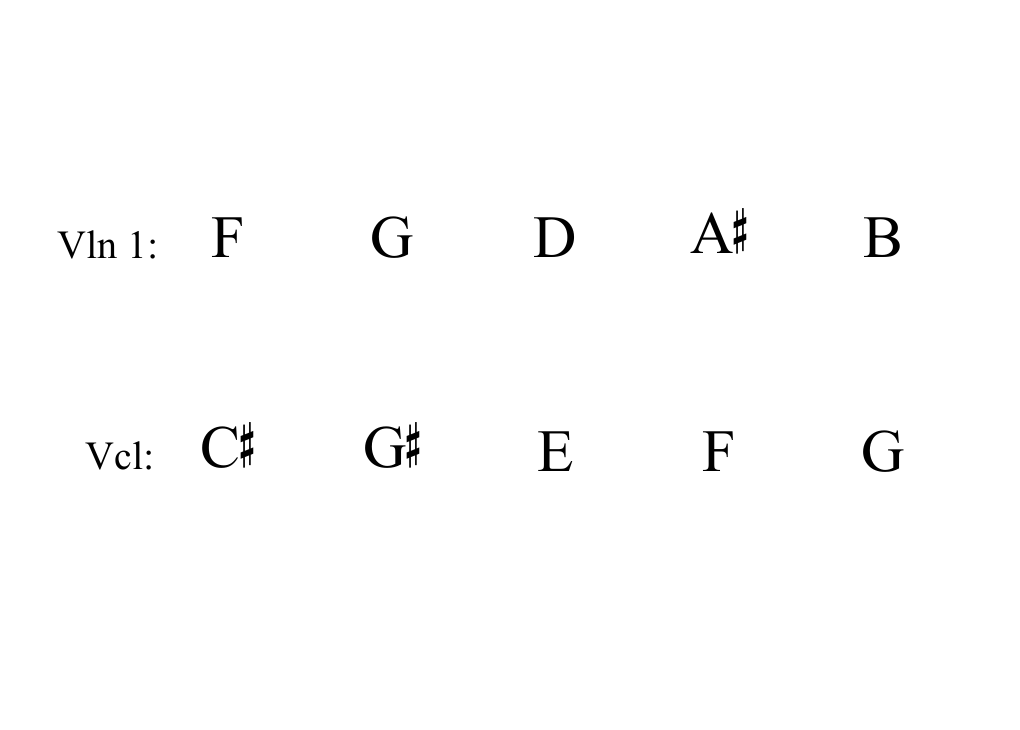
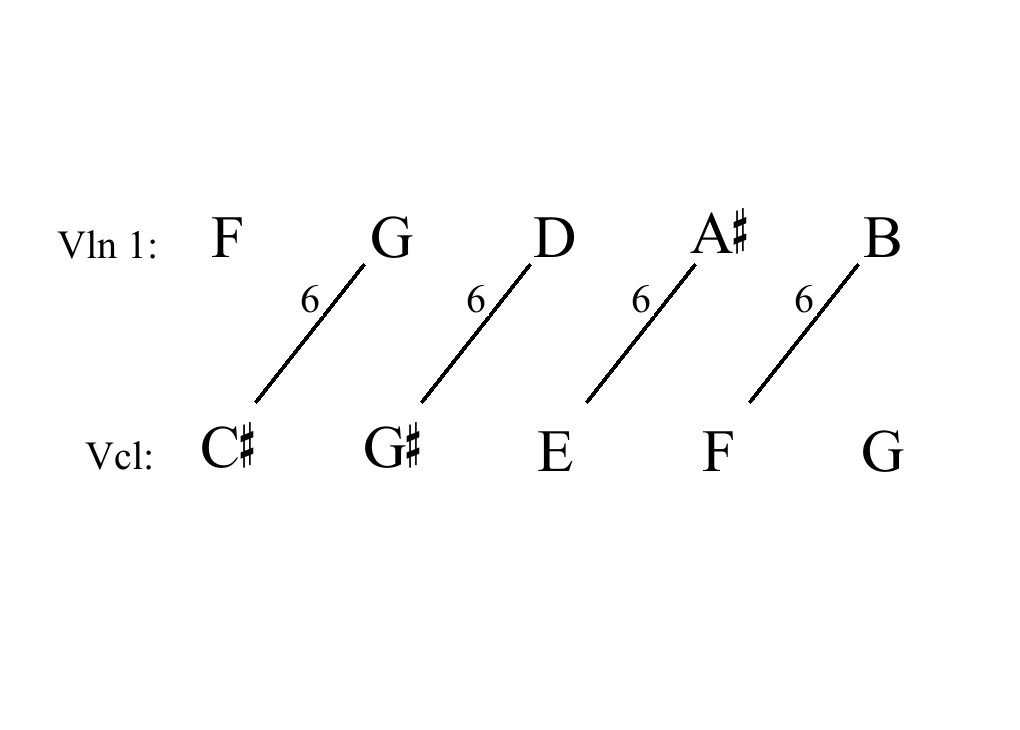
Luciano Berio, Sequenza IXb for E-flat alto saxophone, Rehearsal A

Berio, Sequenza IXb, annotated
[03] dyads marked above, and [06] dyads below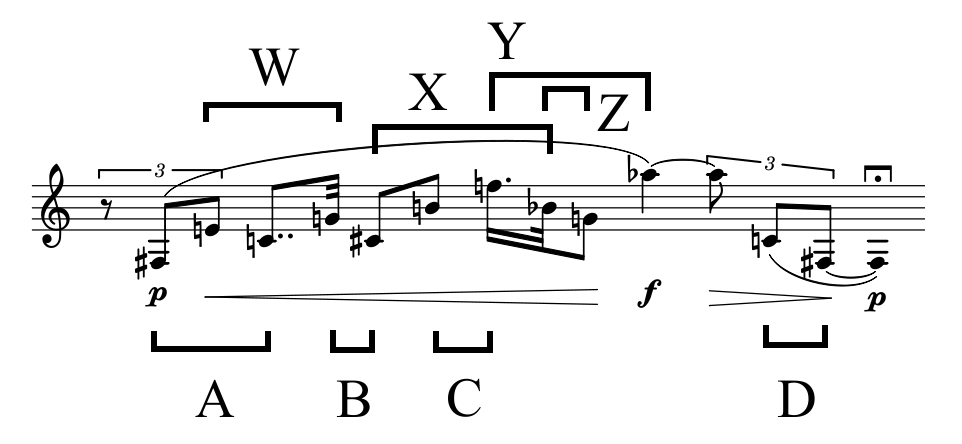
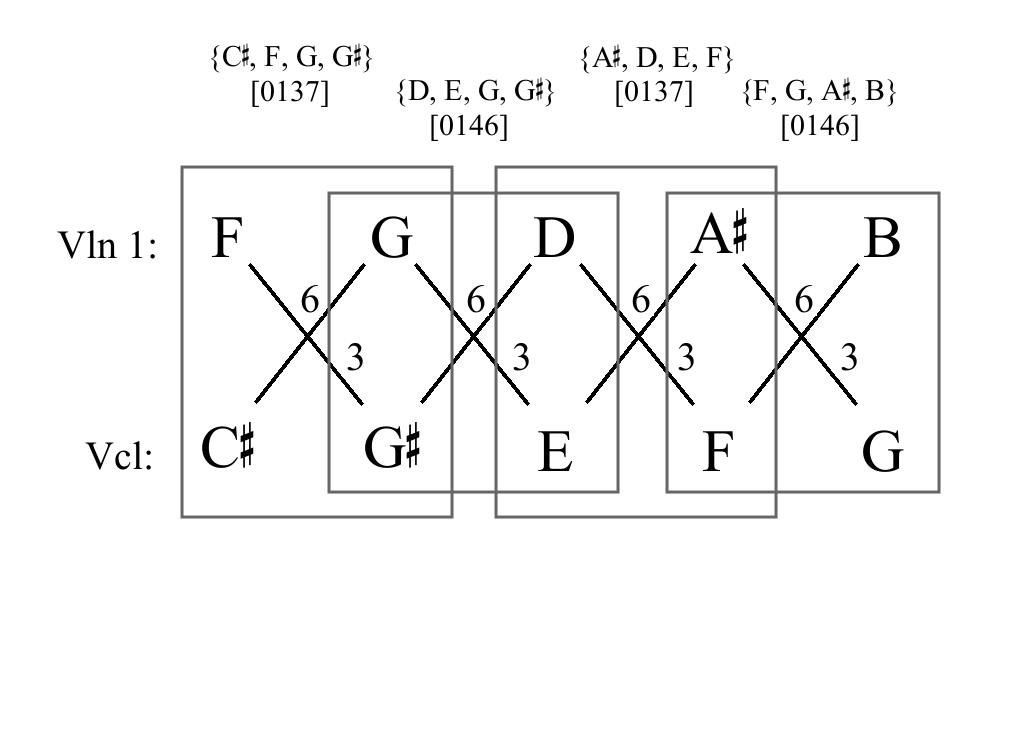
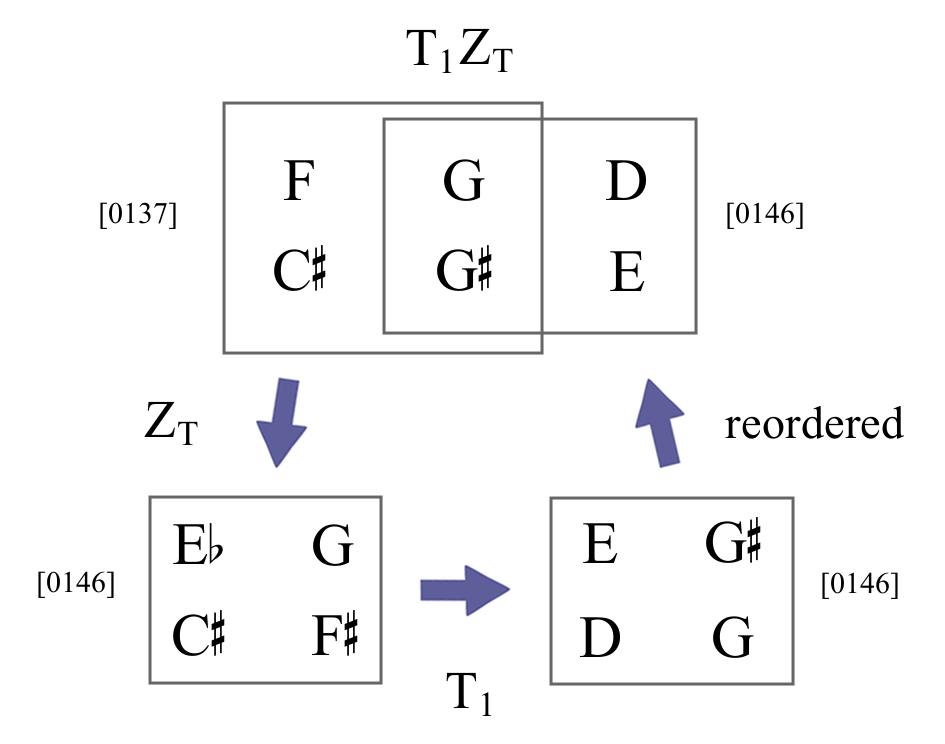
ZT-related pair of AITs
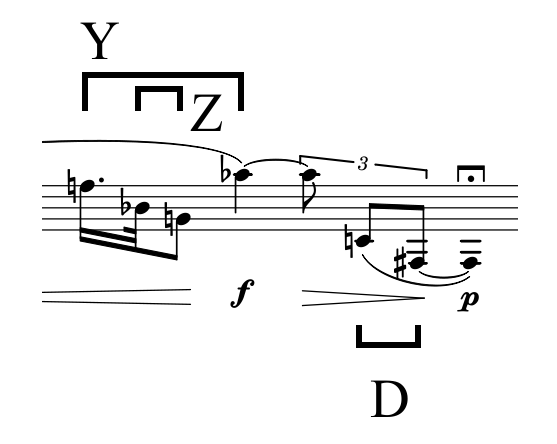
DY = {F♯, C} ∪ {F♮, A♭} = [0137]
DZ = {F♯, C} ∪ {G♮, B♭} = [0146]
ZCS-related pair of AITs
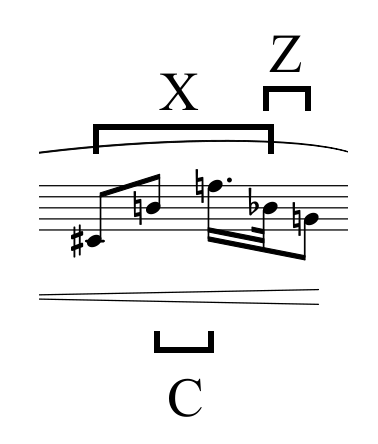
CX = {B♮, F} ∪ {B♭, C♯} = [0137]
CZ = {B♮, F} ∪ {G♮, B♭} = [0146]
{0, 6} ⊎ x + {0, 3} Z {0, 6} ⊎ x + CS{0, 3} if x ≢ 0 (mod3)
[ 0 0 3 6 ]
{0, 6} ⊎ x + {0, 1, 5} Z {0, 6} ⊎ x + CS{0, 1, 5} if x ≢ 0 (mod3)
[ 0 0 1 5 6 ]
Elliott Carter, Fragment no. 2, mm. 11-16.